#단상 회로 전력 : 공급 변압기(전원) 1개
단상 회로
#피상전력 : 변압기에서 나온다.
단상 VI = $I^2Z = \frac{V^2}{Z}$ 단위 : VA
$피상전력 = \sqrt {유효전력^2 + 무효전력 ^2}$
#유효전력 : 저항
단상 VIcosΘ = $I^2R = \frac{V^2}{R}$ 단위: W
소비전력 = 유효전력 = 부하전력 = 평균전력
#무효전력 : 콘덴서, 코일에서 나온다.
단상 VISinΘ = $I^2X$ = $\frac{V^2}{X}$ = $유효전력 \times {\frac{ cosΘ }{sinΘ}}$ 단위: Var
#역률
역률 = $유효전력 \over 피상전력$
부하를 직렬접속시 $cosΘ = {R \over \sqrt {(R^2+X^2)}} = {R \over Z}$
부하를 병렬접속시 $sinΘ = {X \over \sqrt {(R^2+X^2)}} = {X \over Z}$
#삼(3)상 회로의 전력 : 공급 변압기(전원) 3개
#유효전력
P =3 x 상전압 x상전류 x cosΘ = $\sqrt{3}\times선간전압\times선간전류$ = $3\times상전류^2 \times R$ 단위 [W]
#무효전력
Q =3x상전압x상전류xsinΘ = $\sqrt{3}\times선간전압\times선간전류$ = 3x$상전류^2$xX 단위 [Var]
#피상전력
$P_a$ =3x상전압x상전류 = $\sqrt{3}\times선간전압\times선간전류$ = 3x$상전류^2$xZ = $\sqrt{P^2+Q^2}$ 단위 [VA]
3상 회로
3상 회로
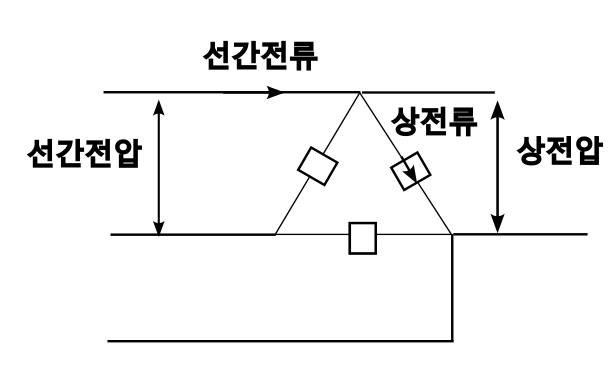3상 부하
n상 회로 전력 : 공급 변압기(전원) n개
유효전력
P=nx상전압x상전류xcosθ = $\frac{n}{2sin{\frac{π}{n}}}$x선전압x선전류xcosθ
V결선 회로 전력 : 공급 변압기 (전원) 2개
유효전력
P= $\sqrt3$ VIcosθ
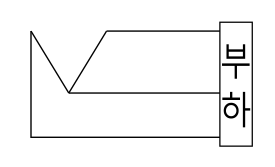V결선 회로
#최대전력 전달 조건
- 최대전력 전달 조건 : 선로측 저항과 부하 저항이 동일한 경우
- 선로측 저항이 복소수로 주어질 경우 : 선로 저항의 공액복소수 값
#$피상전력^2=유효전력^2+무효전력^2$
수전단의 전력원 방정식이 $Pr^2+(Qr+400)^2 = 250000$으로 표현되는 전력계통에서
조상설비 없이 전압을 일정하게 유지하면서 공급할 수 있는 부하전력은?
(단, 부하는 무유도성이다.)
정답 : 300
풀이 :
조상설비 없이 Qr =0
$Pr^2+400^2 = 250000$
출처 : 전기기사 필기 시험 전력공학2020-1.2
[ 예제 문제 ]
역률 80%, 500kVA의 부하설비에 100kVA의 진상용 콘덴서를 설치하여 역률을 개선하면 수전점에서의 부하는 약 몇 kVA가 되는가 ? <실기>
더보기
정답 : 대략 450
풀이 :
1) 유효전력 P = Pacosθ = 500x0.8 =400 [kW]
2) 무효전력
- 콘덴서 설치 전
Pr = Pasinθ = 500x$\sqrt{1-0.8^2}$ = 300 [kVar]
- 콘덴서 설치 후
Pr2 = 300 - 100 = 200
3) 피상전력 $ \sqrt {400^2+200^2}$ ≒ 450 [kVA]
출처 : 전기기사필기시험 전력공학 2019-3회
> 어떤 회로에서 유효전력 80[W], 무효전력 60[Var] 일 때 역률은?
더보기
>정답: 80%
>풀이:
1) $피상전력 = \sqrt {유효전력^2 + 무효전력 ^2}$
$피상전력 = \sqrt {( 80^2 + 60^2)}$ = 100 [VA]
2) $역률= {유효전력 \over 피상전력}\times100 $
$ {80 \over 100} \times 100 = 80$
> 역률 0.8, 800W 단상부하에서 30분간의 무효전력량[Varh]은 얼마인가?
더보기
>정답 : 300 [Varh]
>풀이:
- 유효전력 = VIcosΘ
800= VIx0.8 ∴ 피상전력=VI = 800/0.8 = 1000
2. sinΘ = $ \sqrt{1-0.8^2}$ = 0.6
3. 무효전력 = VIsinΘ
$무효전력 = 피상전력\times sinΘ = 1000 \times 0.6 = 600$ [var]
무효전력량 = 600 x 0.5 = 300 [Varh]
> 어떤 회로에 전압을 115V 인가하였더니 유효전력이 230 W, 무효전력이 345 Var를 지시했다면 회로에 흐르는 전류는 약 몇 A 인가?
더보기
>정답 : 대략 3.6
>풀이 :
$피상전력 = \sqrt {( 230^2 + 345 ^2)}$
$I = 피상전력/115$
> 역률 0.85의 부하 350kW에 50kW를 소비하는 동기 전동기를 병렬로 접속하여 합성 부하의 역률을 0.95로 개선하려면
진상 무효 전력은 약 몇 kVar인가?
더보기
정답 : 85
풀이 :
P = 350+50 = 400[kW] : 병렬로 접속
Pr = 피상전력x 무효율= ${ 350 \over 0.85 } \sqrt {1-0.85^2} = 216.91$ [kVar]
$cosΘ = {P \over \sqrt {(P^2+(Pr-Q)^2)}} = 0.95$
∴ Q ≒85
출처: 전기기사 필기 17-05-07
> 평형 3상 Δ 결선 부하의 각 상의 임피던스가 Z=8+j6[Ω ] 인 회로에 대칭 3상 전원 전압 100[V]를 가할 때 무효율과 무효전력[Var]은?
더보기
>정답 : 무효율 : 0.6 무효전력 : 1800Var
>풀이 :
무효율 = 1- 유효율
$유효율 = {8 \over \sqrt {(8^2+6^2)}}$
무효전력
$Pr = 3I^2X = 3(\frac{V}{Z})^2X $
$3({100\over \sqrt {8^2+6^2}})^2 \times 6 = 1800[var]$
출처: 전기기사 필기 14-3 회로이론 및 제어공학
> 어떤 회로에 E=100+j50[v]인 전압을 가했더니 I=3+j4인 전류가 흘렀다면 이 회로의 소비전력[W]은?
더보기
>정답: 500
>풀이:
(100-j5)(3+j4) = 500+j250
출처: 전기기사 필기 2013-3회 회로이론 및 제어공학
> 부하 역률이 현전히 낮은 경우 발생하는 현상이 아닌 것은?
- 전기 요금의 증가
- 유효 전력의 증가
- 전력 손실의 증가
- 선로의 전압강하 증가
더보기
정답 : 2
풀이 :
유효전력 = 피상전력 x 역율
> 대칭 3상 Y부하에서 각상의 임피던스가 Z=3+j4[Ω] 이고, 부하 전류가 20[A]일 때 이 부하의 무효전력[Var]은?
더보기
정답 : 4800[Var]
풀이 : $3I^2X=3\times20^2\times4 = 4800[Var]$
> 1상의 임피던스가 Z=20+j10[Ω]인 Y결선 부하에 대칭 3상 선간전압 200[V]를 인가했을 때 소비되는 유효전력은 얼마인가?
더보기
정답 : 1.6[kW]
풀이 :
Y결선의 상전압 $Vp = \frac{200} {\sqrt(3)} = 115.47[v]$
상전류 $Ip=\frac{115.47}{\sqrt (20^2+10^2)}=5.16[A]$
$P=3I^2R=3\times5.16^2\times20\times10^-3=1.6$[kW]
>단상 전력계 2개로 3상 전력을 측정하고자 한다. 전력계의 지시가 각각 200[w], 100[w]를 가리켰다고 한다. 부하의 역률은 약 몇%]인가?
더보기
정답 : 86.6
풀이 :
$ cosΘ = \frac{(200+100)}{ 2\sqrt{200^2+100^2-200\times100}} = 0.866$
> 수전단의 전력원 방정식이 $Pr^2+(Qr+400)^2 = 250000$으로 표현되는 전력계통에서 가능한 최대로 공급할 수 있는 부하전력 Pr과 이때 전압을 일정하게 유지하는데 필요한 무효전력 Qr은 각각 얼마인가?
더보기
정답: Pr = 500, Qr = -400
풀이:
- 최대로 부하전력을 공급하려면 무효전력이 0이어야 한다. 따라서 $Pr^2+0 = 500^2$ Pr = 500
- 전압을 일정하게 유지하기 위해서는 피상전력의 크기가 일정해야 한다.
$500^2+(Qr+400)^2 = 250000$에서 Qr =-400
